Cosmologists generally agree that our universe is flat. But how exactly can that be for our 3-dimensional selves and everything else for that matter? Well, first it’s useful to note that the flatness is a property of geometry, and not topology. So, even though it’s flat, the universe could be folded and/or twisted in any number of different, esoteric ways.
From Space:
The universe is flat. But there’s a lot of subtlety packed into that innocent-looking statement. What does it mean for a 3D object to be “flat”? How do we measure the shape of the universe anyway? Since the universe is flat, is that…it? Is there anything else interesting to say?
Oh yes, there is.
First, we need to define what we mean by flat. The screen you’re reading this on is obviously flat (I hope), and you know that the Earth is curved (I hope). But how can we quantify that mathematically? Such an exercise might be useful if we want to go around measuring the shape of the whole entire universe. [The History & Structure of the Universe (Infographic)]
One answer lies in parallel lines. If you start drawing two parallel lines on your paper and let them continue on, they’ll stay perfectly parallel forever (or at least until you run out of paper). That was essentially the definition of a parallel line for a couple thousand years, so we should be good.
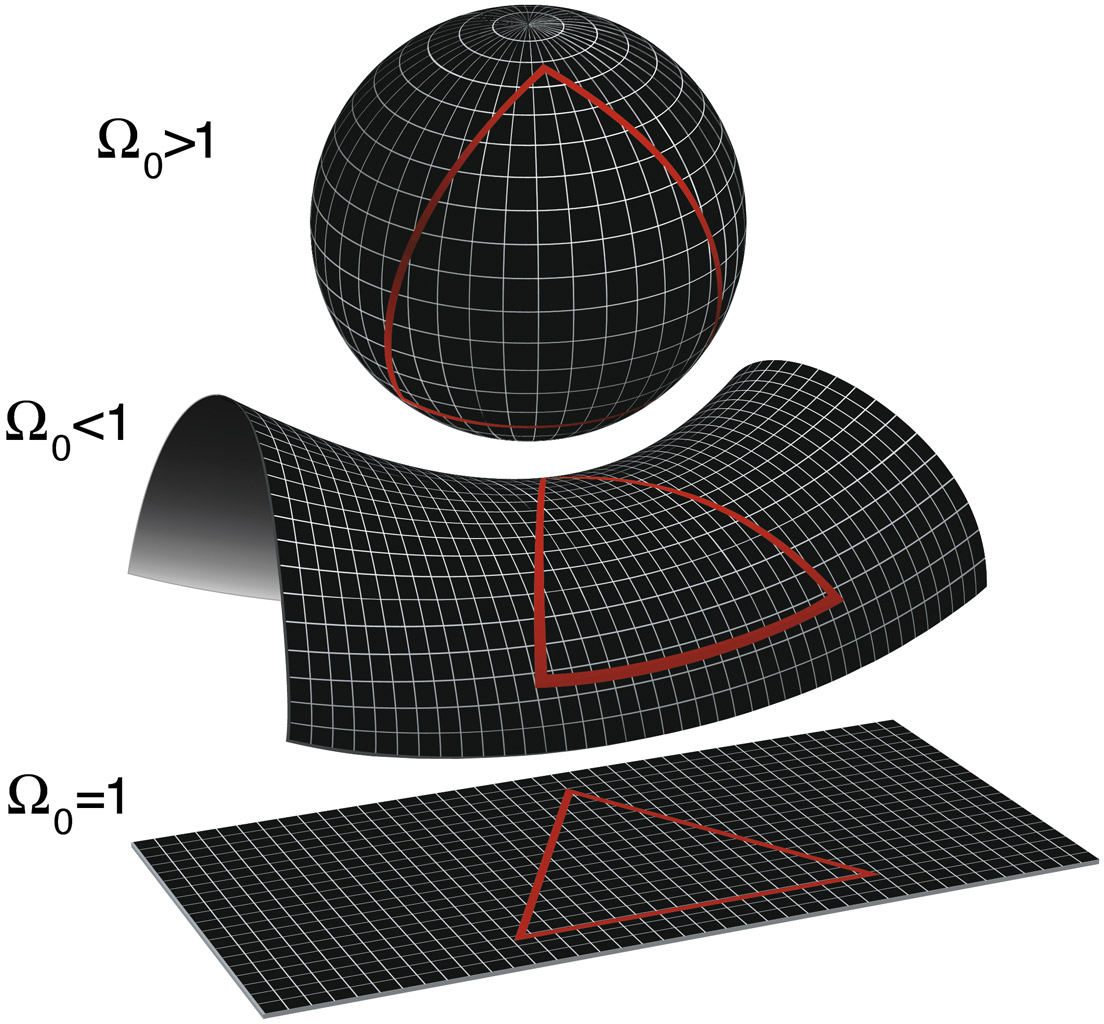
Let’s repeat the exercise on the surface of the Earth. Start at the equator and draw a couple parallel lines, each pointing directly north. As the lines continue, they never turn left or right but still end up intersecting at the North Pole. The curvature of the Earth itself caused these initially parallel lines to end up not-so-parallel. Ergo, the Earth is curved.
The opposite of the Earth’s curved shape is a saddle: on that surface, lines that start out parallel end up spreading apart from each other (in swanky mathematical circles this is known as “ultraparallel”).
Read the entire article here.
Image: The shape of the universe depends on its density. If the density is more than the critical density, the universe is closed and curves like a sphere; if less, it will curve like a saddle. But if the actual density of the universe is equal to the critical density, as scientists think it is, then it will extend forever like a flat piece of paper. Courtesy: NASA/WMAP Science team.
