topology | theDiagonal

universe-shape

Cosmologists generally agree that our universe is flat. But how exactly can that be for our 3-dimensional selves and everything else for that matter? Well, first it’s useful to note that the flatness is a property of geometry, and not topology. So, even though it’s flat, the universe could be folded and/or twisted in any number of different, esoteric ways.

From Space:

The universe is flat. But there’s a lot of subtlety packed into that innocent-looking statement. What does it mean for a 3D object to be “flat”? How do we measure the shape of the universe anyway? Since the universe is flat, is that…it? Is there anything else interesting to say?

Oh yes, there is.

First, we need to define what we mean by flat. The screen you’re reading this on is obviously flat (I hope), and you know that the Earth is curved (I hope). But how can we quantify that mathematically? Such an exercise might be useful if we want to go around measuring the shape of the whole entire universe. [The History & Structure of the Universe (Infographic)]

One answer lies in parallel lines. If you start drawing two parallel lines on your paper and let them continue on, they’ll stay perfectly parallel forever (or at least until you run out of paper). That was essentially the definition of a parallel line for a couple thousand years, so we should be good.

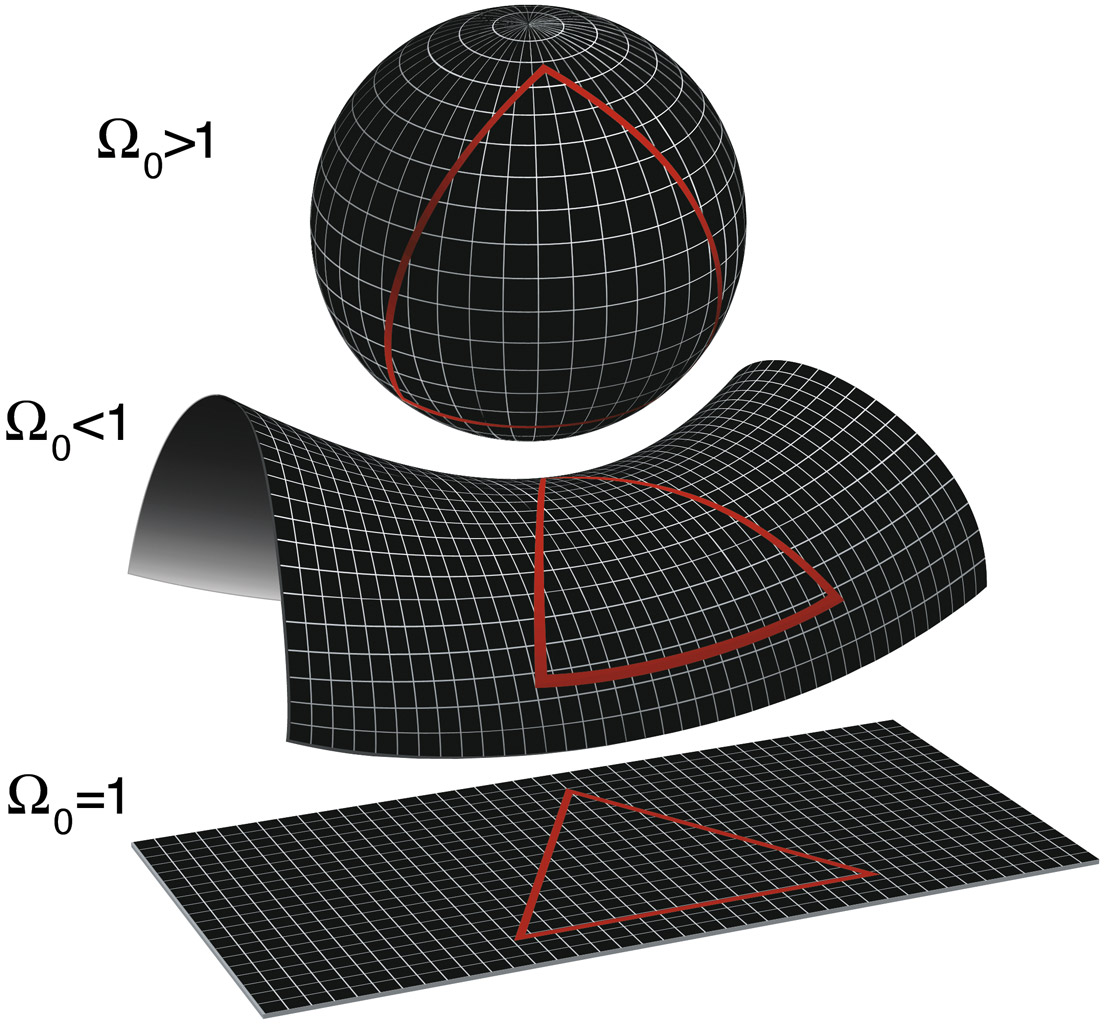
Let’s repeat the exercise on the surface of the Earth. Start at the equator and draw a couple parallel lines, each pointing directly north. As the lines continue, they never turn left or right but still end up intersecting at the North Pole. The curvature of the Earth itself caused these initially parallel lines to end up not-so-parallel. Ergo, the Earth is curved.

The opposite of the Earth’s curved shape is a saddle: on that surface, lines that start out parallel end up spreading apart from each other (in swanky mathematical circles this is known as “ultraparallel”).

Read the entire article here.

Image: The shape of the universe depends on its density. If the density is more than the critical density, the universe is closed and curves like a sphere; if less, it will curve like a saddle. But if the actual density of the universe is equal to the critical density, as scientists think it is, then it will extend forever like a flat piece of paper. Courtesy: NASA/WMAP Science team.

Your friends have more friends than you. But wait there’s more not-so-good news. Not only are your friends friendlier and befriended more than you, they are also likely to be wealthier and happier. How can this be, you may ask? It’s all down to averaging and the mathematics of networks and their interconnections. This so-called Friendship Paradox manifests itself in the dynamics of all social networks — it applies online as well as in the real world.

From Technology Review:

Back in 1991, the sociologist Scott Feld made a surprising discovery while studying the properties of social networks. Feld calculated the average number of friends that a person in the network has and compared this to the average number of friends that these friends had.

Against all expectations it turned out that the second number is always bigger than the first. Or in other words, your friends have more friends than you do.

Researchers have since observed the so-called friendship paradox in a wide variety of situations. On Facebook, your friends will have more friends than you have. On Twitter, your followers will have more followers than you do. And in real life, your sexual partners will have had more partners than you’ve had. At least, on average.

Network scientists have long known that this paradoxical effect is the result of the topology of networks—how they are connected together. That’s why similar networks share the same paradoxical properties.

But are your friends also happier than you are, or richer, or just better? That’s not so clear because happiness and wealth are not directly represented in the topology of a friendship network. So an interesting question is how far the paradox will go.

Today, we get an answer thanks to the work of Young-Ho Eom at the University of Toulouse in France and Hang-Hyun Jo at Aalto University in Finland. These guys have evaluated the properties of different characteristics on networks and worked out the mathematical conditions that determine whether the paradox applies to them or not. Their short answer is yes: your friends probably are richer than you are.

The paradox arises because numbers of friends people have are distributed in a way that follows a power law rather than an ordinary linear relationship. So most people have a few friends while a small number of people have lots of friends.

It’s this second small group that causes the paradox. People with lots of friends are more likely to number among your friends in the first place. And when they do, they significantly raise the average number of friends that your friends have. That’s the reason that, on average, your friends have more friends than you do.

But what of other characteristics, such as wealth and happiness, which are not represented by the network topology?

To study other types of network, Eom and Jo looked at two academic networks in which scientists are linked if they have co-authored a scientific paper together. Each scientist is a node in the network and the links arise between scientists who have been co-authors.

Sure enough, the paradox raises its head in this network too. If you are a scientist, your co-authors will have more co-authors than you, as reflected in the network topology. But curiously, they will also have more publications and more citations than you too.

Eom and Jo call this the “generalized friendship paradox” and go on to derive the mathematical conditions in which it occurs. They say that when a paradox arises as a result of the way nodes are connected together, any other properties of these nodes demonstrate the same paradoxical nature, as long as they are correlated in certain way.

As it turns out, number of publications and citations meet this criteria. And so too do wealth and happiness. So the answer is yes: your friends probably are richer and happier than you are.

That has significant implications for the way people perceive themselves given that their friends will always seem happier, wealthier and more popular than they are. And the problem is likely to be worse in networks where this is easier to see. “This might be the reason why active online social networking service users are not happy,” say Eom and Jo, referring to other research that has found higher levels of unhappiness among social network users.

So if you’re an active Facebook user feeling inadequate and unhappy because your friends seem to be doing better than you are, remember that almost everybody else on the network is in a similar position.

Read the entire article here.

Image: Cast of the CBS TV show Friends. Courtesy of Vanity Fair, CBS and respective rights holders.

theDiagonal

Tag Archives: topology

We Live in a Flat Universe