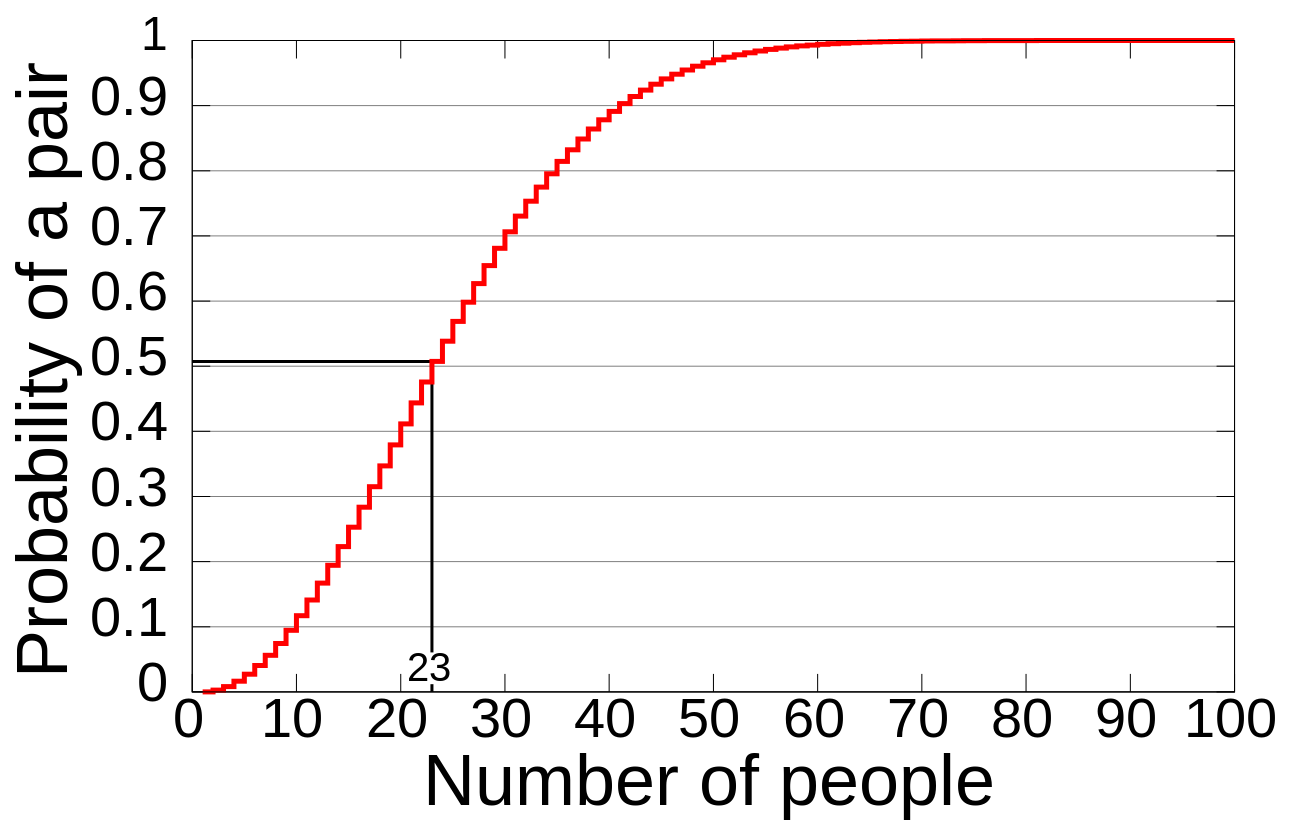
I first came across the Birthday Problem in my first few days of my first year of secondary school in London [that would be 6th grade for my US readers]. My mathematics teacher at the time realized the need to discuss abstract problems in concrete terms, especially statistics and probability. So, he wowed many of us — in a class of close to 30 kids — by firmly stating that there was a better than even chance that two of us shared the same birthday. In a class of 30, the actual probability is 60 percent, and rises to close to 100 percent is a group of only 60.
Startlingly, two in our class did indeed share the same birthday. How could that be possible, I wondered?
Well, the answer is grounded in the simple probability of large populations. But, it is also colored by our selective biases to remember “remarkable” coincidences and to ignore the much, much larger number of instances where there is no coincidence at all.
From the Washington Post.
Mathematician Joseph Mazur was in the back of a van snaking through the mountains of Sardinia when he heard one of his favorite coincidence stories. The driver, an Italian language teacher named Francesco, told of meeting a woman named Manuela who had come to study at his school. Francesco and Manuela met for the first time in a hotel lobby, and then went to have coffee.
They spoke for an hour, getting acquainted, before the uncomfortable truth came out. Noting Manuela’s nearly perfect Italian, Francesco finally asked why she decided to come to his school.
“She said, ‘Italian? What are you talk about? I’m not here to learn Italian,’” Mazur relates. “And then it dawned on both of them that she was the wrong Manuela and he was the wrong Francesco.” They returned to the hotel lobby where they had met to find a different Francesco offering a different Manuela a job she didn’t want or expect.
The tale is one of the many stories that populate Mazur’s new book, “Fluke,” in which he explores the probability of coincidences.
Read the entire article here.
Image: The computed probability of at least two people sharing a birthday versus the number of people. Courtesy: Rajkiran g / Wikipedia. CC BY-SA 3.0.
